Establecer relaciones de orden entre números racionales
Una de las maneras en que podemos posicionar los números racionales en la recta numérica es a través de la conversión de decimales a fracción.
Para aprender de este tema haz click aquí
Pierce, Rod. "Convertir Decimales a Fracciones" Disfruta Las Matemáticas. Ed. Rod Pierce. 5 Oct 2011. 19 Dec 2011
Transformación de un decimal finito a fracción
Se convierte el número a fracción decimal y, si se puede, se simplifica. Para transformar el número decimal a fracción decimal se utilizan potencias de diez (10, 100, 1.000, etc.). Se colocan tantos ceros como cifras decimales tenga el número.
Ejemplo 1:
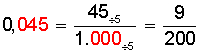
Se anota el número, en este caso 45. Se divide por 1.000, porque hay tres espacios decimales ocupados, luego simplificamos por 5
Ejemplo 2:
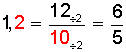
Transformación de un decimal infinito periódico en fracción
Los pasos a seguir son los siguientes:
1) Se anota el número y se le resta él o los números que están antes del período (de la rayita)
2) Se coloca como denominador un 9 por cada número que está en el período (si hay un número bajo la rayita se coloca un 9, si hay dos números bajo el período se coloca 99, etc.). Si se puede simplificar, se simplifica.
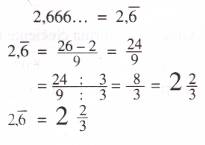
Otro ejemplo: Expresar como fracción 57,18181818....
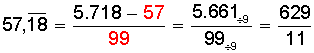
Transformación de decimal infinito semiperiódico a fracción
1) El numerador de la fracción se obtiene, al igual que en el caso anterior, restando al número la parte entera y el anteperíodo, o sea, todo lo que está antes de la “rayita”.
2) El denominador de la fracción se obtiene colocando tantos 9 como cifras tenga el período y tantos 0 como cifras tenga el anteperíodo. Como siempre, el resultado se expresa como fracción irreductible (no se puede simplificar más) o como número mixto.

Fuente : Profesor en línea
Continuará ... tema en construcción

No hay comentarios:
Publicar un comentario